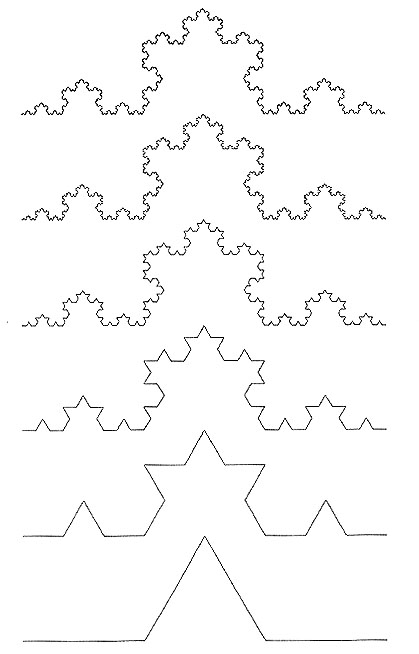
ZIELE

THEMA DER PHASE 7

In der letzten Übung haben Sie ein Vokabular ume ein Elemente erweitert. Ein Kriterium hierfür war, das ganze Vokabular als einen Baukasten zu verstehen, mit Elementen, die sich gut kombinieren lassen. In dieser Phase können Sie nun mit so einem Baukasten ein neues Objekt aufbauen. Für die Gesamtkonstellation des Objektes ist die Beziehung der Teile zum Ganzen wesentlich.

Die Beziehung vom Teil zum Ganzen ist ein sehr wichtiges architektonisches Thema. In Palladio´s Quattro Libri steht: ,,Schönheit entspringt der schönen Form und der Entsprechung des Ganzen mit den Einzelteilen, wie der Entsprechung der Teile untereinander und dieser wieder zum Ganzen, so dass das Gebäude wie ein einheitlicher und vollkommener Körper erscheint."

Eine Beziehung vom Teil zum Ganzen kann auf verschiedene Weise sinnfällig gemacht werden. In dieser Übung sollen Sie versuchen, das ganze Objekt zu einer formalen Einheit zu machen, indem Sie der Gesamtgestalt ein gewisses Mass an Ähnlichkeit mit Ihren Bestandteilen geben. Dadurch wird, wenn Sie es geschickt anstellen, eine Selbstähnlichkeit des Objektes und seiner Bestandteile resultieren, die dem Objekt eine "natürliche", stimmige Ausstrahlung verleiht.

Um das Verhältnis des Teils zum Ganzen, bzw. um Selbstähnlichkeit geht es auch in der Fraktalen Geometrie.

Fraktale

Die fraktale Geometrie erlaubt es, natürliche Formen mathematisch zu beschreiben und chaotische Systeme bildlich zu veranschaulichen. Ein bekanntes Fraktal ist jede Küstenlinie. Betrachtet man einen immer kleineren Ausschnitt der Küste, zeigen sich in jedem Schritt mehr Buchten und Halbinseln. Mit jedem Fels oder Sandkorn wiederholen sich dieselben selbstähnlichen Muster und die Gesamtlänge wächst gegen Unendlich. Neben der Selbstähnlichkeit haben die Fraktale die Eigenschaft der Nichtlinearität: eine Küstenlinie kann nicht mit den Instrumenten der euklidischen Geometrie, der eindimensionalen Geraden oder der zweidimensionalen Fläche beschrieben werden. Die Dimension der Küstenlinie ist grösser als eins, aber kleiner als zwei. Sie entspricht damit einer gebrochenen Zahl zwischen eins und zwei, daher der Name Fraktal.

Ein bekannter Ansatz ist Mandelbrots Arbeit über die fraktale Geometrie der Natur, in der die Relevanz rekursiv definierter Formen und Kurven für viele Wissenschaftsbereiche deutlich wird. Wie Mandelbrot nachweist, sind fast alle natürlichen Formen durch fraktale Algorithmen darstellbar. Er findet die Architektur der Beaux Arts-Periode reich an fraktalen Aspekten, nicht aber die Architektur Mies van der Rohes (worüber sich allerdings durchaus streiten liesse). Die Untersuchung der fraktalen Geometrie der Architektur ist spätestens seit den Bauten von Sullivan oder in jüngerer Zeit von Eisenmann ein Thema geworden, das immer wieder in architekturtheoretischen Diskussionen auftaucht. Peter Eisenmann zum Beispiel behauptet von sich, ein "fraktaler Denker" zu sein.