In dieser Phase kommen sämtliche in den letzten drei Übungen
im Zusammenhang mit Types & Instances eingeführten Konzepte,
also Entwurfsvokabular, Substitution, Detaillierungsgrad und Hierarchische
Strukturen, zum Einsatz. Mit diesen Mitteln soll ein Modell mit
einer selbstähnlichen Struktur entwickelt werden. Als Hintergrund
dazu wird das Thema der fraktalen Geometrie eingeführt.

Fig. 8.1. Fraktale Geometrie: von Koch Snowflake. Schrittweise
Zunahme der Anzahl der Rekursionen.
In der letzten Übung haben Sie ein Vokabular auf ein vordefiniertes Objekt angewendet. In dieser Phase können Sie nun einen Schritt weiter gehen und auch die Gesamtkonstellation des Objektes selbst bestimmen. Dadurch können Sie die Beziehungen der Teile zum Ganzen, die in der letzten Phase rein zufällig waren, steuern.
Die Beziehung vom Teil zum Ganzen ist ein sehr wichtiges architektonisches Thema. In Palladio´s Quattro Libri steht: „Schönheit entspringt der schönen Form und der Entsprechung des Ganzen mit den Einzelteilen, wie der Entsprechung der Teile untereinander und dieser wieder zum Ganzen, so dass das Gebäude wie ein einheitlicher und vollkommener Körper erscheint."
Eine durchgängige Gestaltung im selben Geist von der städtebaulichen Lösung bis zum Treppengeländer gilt auch heute als wesentliches Merkmal guter Architektur.
Eine Beziehung vom Teil zum Ganzen kann auf verschiedene Weise sinnfällig gemacht werden. In dieser Übung sollen Sie versuchen, das ganze Objekt zu einer formalen Einheit zu machen, indem Sie der Gesamtgestalt ein gewisses Mass an Ähnlichkeit mit Ihren Bestandteilen geben. Dadurch wird, wenn Sie es geschickt anstellen, eine Selbstähnlichkeit des Objektes und seiner Bestandteile resultieren, die dem Objekt eine "natürliche", stimmige Ausstrahlung verleiht.
Um das Verhältnis des Teils zum Ganzen, bzw. um Selbstähnlichkeit
geht es auch in der Fraktalen Geometrie.
Fraktale
Die fraktale Geometrie erlaubt es, natürliche Formen mathematisch
zu beschreiben und chaotische Systeme bildlich zu veranschaulichen.
Ein bekanntes Fraktal ist jede Küstenlinie. Betrachtet man
einen immer kleineren Ausschnitt der Küste, zeigen sich in
jedem Schritt mehr Buchten und Halbinseln. Mit jedem Fels oder
Sandkorn wiederholen sich dieselben selbstähnlichen Muster
und die Gesamtlänge wächst gegen unendlich. Neben der
Selbstähnlichkeit haben die Fraktale die Eigenschaft der
Nichtlinearität: eine Küstenlinie kann nicht mit den
Instrumenten der euklidischen Geometrie, der eindimensionalen
Geraden oder der zweidimensionalen Fläche beschrieben wreden.
Die Dimension der Küstenlinie ist grösser als eins,
aber kleiner als zwei. Sie entspricht damit einer gebrochenen
Zahl zwischen eins und zwei, daher der Name Fraktal.
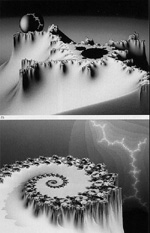
Fig. 8.2, 8.3. Fraktale Landschaften.
Ein bekannter Ansatz ist Mandelbrots Arbeit über die fraktale
Geometrie der Natur, in der die Relevanz rekursiv definierter
Formen und Kurven für viele Wissenschaftsbereiche deutlich
wird. Wie Mandelbrot nachweist, sind fast alle natürlichen
Formen durch fraktale Algorithmen darstellbar. Er findet die Architektur
der Beaux Arts-Periode reich an fraktalen Aspekten, nicht aber
die Architektur Mies van der Rohes (worüber sich allerdings
durchaus streiten liesse). Die Untersuchung der fraktalen Geometrie
der Architektur ist spätestens seit den Bauten von Sullivan
oder in jüngerer Zeit von Eisenmann ein Thema geworden, das
immer wieder in architekturtheoretischen Diskussionen auftaucht.
Peter Eisenmann zum Beispiel behauptet von sich, ein „fraktaler
Denker" zu sein.


Fig. 8.4, 8.5. Selbstähnliches Objekt. Maximilian Ofner,
Wintersemester 1995/96.
Sie erhalten eine leere Zeichnung und eine gleichnamige library.
Mit den Compounds aus der Library können sie ein Modell in
der Formensprache Ihrer Library bauen. Denken sie dabei an die
Themen Selbstähnlichkeit und fraktale Geometrie. Als Ausgangspunkt
für Ihre Komposition können Sie auch ein Objekt nehmen,
das mit der Parameter Engine erstellt wurde oder eines, das bereits
als Compound in Ihrer Library besteht. Sie sollten es danach aber
so modifizieren, dass eine präzise Beziehung der Teile zum
Ganzen entsteht.
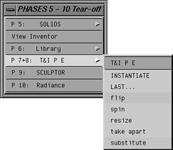
Fig. 8.6. Die Funktionen der Phase 8 im AutoCAD Menu.
Zum Modellieren stehen Ihnen nun sämtliche Operationen, welche im Laufe des Semesters eingeführt wurden, zur Verfügung. Neu hinzukommen die T&I-Befehle SPIN und RESIZE.
Sie können natürlich wiederum Ihre Library mit neuen
Compounds erweitern, um die Hierarchisierung Ihres Modells zu
steigern.
Um die Phase abzuschliessen, müssen Sie eine Komposition
aus Elementen der Ihnen zur Verfügung gestellten Library
erstellen. Dabei soll eine selbstähnliche, hierarchische
Struktur des Modells angestrebt werden, die dem ganzen eine formale
Kohärenz gibt.
Die fertige Komposition halten Sie in Bildern (maximal 5) fest.
In der nächsten Phase wird ein Substrat aus Ihrem Modell,
die Struktur in der Sie die Types angeordnet haben, weiterbearbeitet.
Genauere Angaben über Bildformat und Abgabeprozedur können
Sie der Kurshomepage entnehmen

Fig. 8.7. Innenansicht des Selbstähnlichen Objektes von
Figur 8.4 und 8.5. Maximilian Ofner, Wintersemester 1995/96.
