|
|
||||||||||
| MAS ETH ARCH/CAAD - 2004/05 - STUDENT PAGES Master of Advanced Studies in Architecture, Specialization in Computer Aided Architectural Design | 065-0005/6 Supervision: Prof. Dr. Ludger Hovestadt, Philipp Schaerer Chair of CAAD, ETH Zurich home | Structure | Stage01 | Stage01 - inquestChaost"Bauen mit Maschinen - Das Chaos baubar machen." Chaos: aus dem Griechischen - wirre Urmasse aus der die sichtbare Welt entsteht ... heute vergleichbar mit dem Modell des Urknalls , das Gegenteil von Kosmos in der Mytologie - der ungeordnete ungeformte Weltzustandaus dem am anfang weitere Götter hervorgingen Kosmogonie: Lehre der Erschaffung der Welt Kosmogenie: Lehre der Entstehung der Welt "Chaos ist das Gegenteil von Ordnung. Unordnung ist nur ein anderes Stadium einer Ordnung ... ein Zusammenprall beziehungsloser Einzelordnungen. ... Komplexität ... auch hier ist trotz der Wahrnehmung einer grossen Vielfalt das Gefühl der Möglichkeit einer Beherrschung dieser Vielfalt vorhanden." (Sylvia Stöbe "Chaos und Ordnung in der modernen Architektur") Damit wird Chaos zu einer Zustandsgrösse ähnlich dem absoluten Nullpunkt die teoretisch vorhanden aber nicht erreichbar ist. Die Chaostheorie beschäftigt sich als ein Teilgebiet der Mathematik und Physik mit bestimmten nichtlinearen dynamischen Systemen, die eine Reihe von Phänomenen aufweisen, die man zusammengenommen als Chaos bezeichnet. (Nichtlineare Systeme reagieren auf Störungen, im Gegensatz zu linearen Systemen, nicht proportional. Die meisten in der Natur vorkommenden Systeme sind nichtlinear. Anderes als der spezielle Name vermuten lässt, sollte man eher lineare Phänomene als Spezialfall herausstellen: [In der Physik die nichtlinearen Systeme herauszustellen ist so,] als wollte man den größten Teil der Zoologie als das Studium aller "Nicht-Elefanten" auffassen. (Stanislaw Marcin Ulam) Ein oft benutztes Beispiel ist das Wetter. Eine kleine Störung kann durchaus entscheiden ob es regnet oder ob die Sonne scheint (Schmetterlingseffekt).) Sensitive Abhängigkeit von den Anfangsbedingungen Anders als der Begriff Chaos in der Umgangssprache charakterisiert der Begriff hier nicht den Zustand eines Systems, wie beispielsweise seine Unordnung, sondern sein zeitliches Verhalten, das heißt seine Dynamik. Genau genommen ergibt sich chaotisches Verhalten dann, wenn die aus einer Änderung der Anfangsbedingungen resultierenden Unterschiede in der zeitlichen Entwicklung eines Systems zunächst exponentiell mit der Zeit anwachsen anstatt linear oder polynomial, das System aber beschränkt ist, so dass auch dem Wachstum dieser Unterschiede eine Grenze gesetzt ist. Anhand klassischer Experimente in der Physik Galileis und anderen zeigt sich, dass schon bei geringfügigen Änderungen in den Anfangsbedingungen eines Systems (schwingendes Pendel, das mit den Zustandsvariablen bzw. Parametern Ort, Geschwindigkeit, Luftwiderstand/Dissipation beschrieben wird) große und überraschende Effekte auf den Zustand und die Dynamik des Systems entstehen können. Deterministisches Chaos Deterministisches Chaos ist ein irregulär erscheinendes chaotisches Verhalten, welches jedoch den Regeln einer deterministischen Dynamik folgt (Der Begriff Dynamik (v. griech. dynamiké — mächtig bzw. dynamis — Kraft) bezeichnetallgemein Kraft, Triebkraft oder auf Veränderung gerichtete Kraft. Eine zeitliche Entwicklung wird hiermit in Zusammenhang gebracht. in der Physik die Lehre vom Einfluss der Kräfte auf die Bewegungsvorgänge von Körpern, siehe Dynamik (Physik) in allgemeinen physikalischen oder mathematischen Zusammenhängen den Quotienten aus Maximum und Minimum einer physikalischen Größe oder Funktion, siehe Dynamikumfangin der Systemtheorie die Veränderung und Entwicklung von Systemen, siehe Dynamik (System)). Es wird nicht durch zufällige äußere Umstände, wie beispielsweise dem Rauschen, verursacht. Systeme mit deterministischem chaotischem Verhalten sind demnach nur scheinbar stochastische Systeme (Bei stochastischen Systemen gibt der momentane Zustand des Systems im Gegensatz zu deterministischen (Determinismus (von lateinisch: determinare abgrenzen, bestimmen) ist eine philosophische Denkrichtung und zusammen mit seinem Gegenstück, dem Indeterminismus, ein wesentliches Grundelement zur Herausbildung eines konsistenten Weltbildes. Er geht davon aus, alle Ereignisse liefen nach feststehenden Gesetzen ab und wären durch diese vollständig bestimmt bzw. determiniert. Deterministen sind also der Auffassung, dass bei bekannten Naturgesetzen und dem vollständig bekannten Zustand eines Systems, der weitere Ablauf aller Ereignisse prinzipiell vorherbestimmt ist und folglich weder ein echter Zufall, noch Wunder bzw. ähnliche nicht-physische Phänomene existieren. Dies kann, muss jedoch nicht, eine Berechenbarkeit des Systems zur Folge haben, was unter anderem dessen Vorhersagbarkeit beeinflusst. Es gibt verschiedene Varianten des Determinismus, die mehr oder minder streng die Vorherbestimmtheit aller Ereignisse voraussetzen. Beispielsweise hängt dies davon ab, ob mit dem betrachteten System nur ein Teil des Universums oder das Universum als Ganzes gemeint ist. Auch spielen weitere Postulate wie beispielsweise die Existenz eines Schöpfers bzw. Gottes eine Rolle, wobei jedoch schnell die Gefahr zirkulärer Logik durch sich lediglich gegenseitig rechtfertigende Postulate besteht. Im Zusammenspiel der durch vielfältige Wechselwirkungen geprägten Konzepte von echtem Zufall, Kausalität bzw. Kausalprinzip, Materialismus, freiem Willen, Berechenbarkeit (Chaostheorie, Deterministisches Chaos, Turingmaschine) und zahlreichen weiteren Fragestellungen an der Berührungsstelle zwischen Naturwissenschaft und Philosophie ergibt sich die Basis eines deterministisch geprägten Weltbildes, wobei die Vielfältigkeit dieser Konzepte auch in einer Vielfältigkeit der Ausprägungen solcher Weltbilder resultiert, besonders in Bezug auf die Existenz eines freien Willens. Es ist hierbei jedoch kaum möglich einen spezifisch naturwissenschaftlichen von einem spezifisch philosophischen oder religiösen Determinismus zu unterscheiden, da sie letzten Endes die gleiche Fragestellung beinhalten und sich lediglich methodisch unterscheiden, sich jedoch auch in dieser Methodik gegenseitig vielschichtig durchdringen.) Systemen nur eine Wahrscheinlichkeitsverteilung für die darauffolgenden Zustände an. Es kann also nicht mit Sicherheit vorhergesagt werden, welchen Zustand das System als nächstes annehmen wird. So gesehen kann ein deterministischer Prozess als Grenzfall eines stochastischen Prozesses mit folgender Wahrscheinlichkeitsverteilung aufgefasst werden: 1 für den nächsten vorherbestimmten Zustand 0 alle anderen Zustände). In der Regel kommen heutzutage bei der Analyse von nicht-transienten aperiodischen Vorgängen sowohl statistische Methoden als auch Methoden aus der Chaostheorie zur Anwendung. Um in einer irregulären (zufällig) erscheinenden Zeitreihe deterministisches Chaos zu entdecken werden Methoden, wie die Spektralanalyse mittels Fouriertransformation, Verzögerungsdiagramme (Henon-Abbildung; Enge Paare), Iterierte Funktionensysteme (IFS) und neuronale Netze eingesetzt. Ein einfaches Modellsystem, dessen Lösung deterministisches Chaos zeigen kann, ist die nichtlineare, zeitdiskrete logistische Gleichung. Entropie in der Physik: Im Gegensatz zu den bereits bekannten extensiven Observablen von thermodynamischen Systemen, wie Energie E, Volumen V und Masse m entzog sich die Entropie zunächst dem tieferen Verständnis und ihre Interpretation führt bis in die heutige Zeit zu Mißverständnissen. Das liegt u.a. an der Diskrepanz zwischen Universalität des Begriffs und seiner konkreten Entwicklung am Wirkungsgrad thermischer Maschinen. Die Entropie konnte erst im Rahmen der statistischen Mechanik von Ludwig Boltzmann befriedigend als Maß für das Phasenraumvolumen erklärt werden, das von der Phasentrajektorie des Systems unter Einhaltung der Konstanz ausgewählter makroskopischer Observabler, wie Temperatur T, Volumen V oder Teilchenzahl N, erreicht werden kann. Anschaulich ist die Entropie demnach ein Maß für fehlende Information über den tatsächlichen Mikrozustand, wenn lediglich eine geringe Anzahl beobachtbarer Größen zur Charakterisierung des Makrozustands vorliegen. Die Entropie ist ein Maß für Unwissenheit, nicht etwa Unordnung. Die Entropie bleibt nur dann unverändert, wenn die Prozesse reversibel verlaufen. Reale Zustandsänderungen sind immer mit Energieverlusten (z.B. durch Reibung) verbunden, wodurch sich die Entropie erhöht. Eine Verringerung der Gesamtentropie in einem geschlossenen System ist nicht möglich. Neben ihrer Rolle als fundamentale Zustandsgröße der phänomenologischen und statistischen Thermodynamik wird die Entropie in anderen Gebieten, insbesondere in der Informationstheorie und in der Wirtschaftswissenschaft benutzt. Die Entropie besitzt in diesen Gebieten eine eigenständige Bedeutung, dieser Unterschied sollte aber nicht überbewertet werden, da letztendlich alle physikalischen Systeme thermodynamisch beschrieben werden können, sobald die Anzahl an Freiheitsgraden ansteigt und Defizite an mikroskopischer Information vorliegen. Quelle: Wikipedia Entropy: http://mats.gmd.de/~skaley/pwc/entropy/Entropy.html Harmonograph http://www.users.globalnet.co.uk/~ngo/ast00800.htm * 1.gif: 
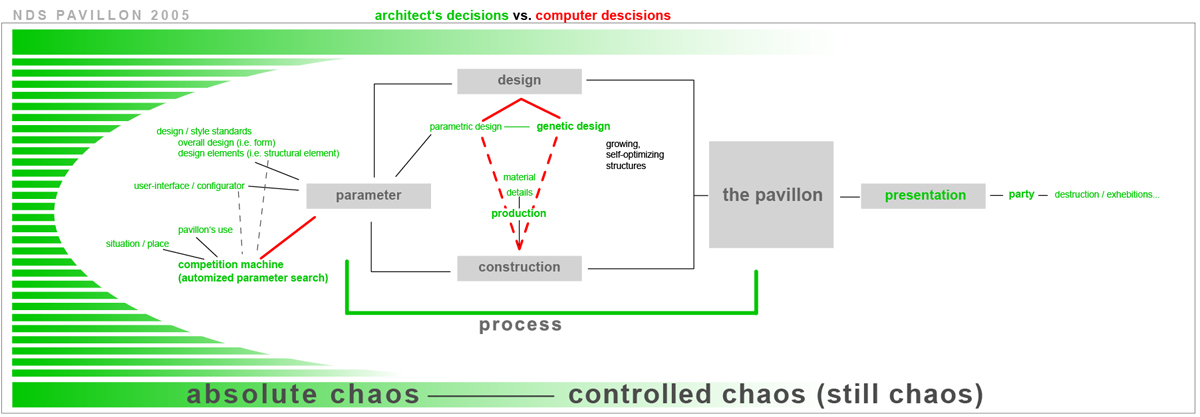

proposition basic approach tb
Methodgenerative design processing genetic growth and evolutionthis means generating space and not just a structure or mere optimising it further keywordsadaptation, optimisation
phenomena-growth-evolution -time -movement -selforganisation -transformation 
image bonsaigrowing organismimpose restrictions by human steering growth 
example genr8surface grows according to parameters and internal algorithmlimitations can be set throug boundaries direction of growth can be controlled by forcefields 
worldwide dispersiongrowing stem cellsbasic approach AS dimensionally unstable structure changes in density to grow or shrink, high density achieves compact and stable structure low density spreads structure to gain ridicolous size optimization in context of purpose, structure "knows" usage and necessary parameters to achieve stable mode evolving, mutating evolution implies reactiveness to the the environment, self-interpretation, basic "intelligence" 


Und dann bin ich aufgewacht.... aaaaahhhhhhhh group thesis Vorschlag PS: 1. form and node pattern generator 2. materialisation, cam-strategy 3. envelope types 4. feature types 5. configurator „more how than what“ „a design-process with different phases in which the computer has a specific task“ (combination of several solutions) “a controlled experiment with an open outcome” “zeigen was möglich ist” structure + envelope (skin) + interactive feature “a generated and customized network structure” .z.B. Projekt Airport: Ich habe die folgenden Gfz, Grz, Abstandsflächen, Raumprogramm >siehe Kaisersrot. Ich möchte ein Gebäude mit minimaler Aussenfläche, durchgehender Tragstruktur mit AchsmassX?, minimaler Aufbauhöhe der abgehängten Decke usw...Welche Einwirkungen hat das jeweils auf die Anzahl von Höhe, Stockwerke, Statik, Lifts, Lüftung, Volumen, Flächen, Preis des Gebäudes, Verhältniss Fläche/Preis, Fluchtwege, Marktwert, Fassadenflächen, Wandflächen, Zeitaufwand.......und bei angewendetem Detail...m2 Glas, lfm Pressleiste, m2 Trockenbauwände, m3 Stahl, m3 Beton, Anzahl der Leuchten pro Stockwerk, Personen pro Stockwerk, Parkplätze, Wärme + Kühllasten, Wärmedurchgangskoeffizienten, Brandlasten.......Welche Anforderung stellen sich damit an Lebensdauer und Qualität der Materialien und Details und wie beinflusst dies wiederrum das Raumprogramm, damit das Volumen, damit den Preis und damit die angestrebte Lebensdauer. Jeder dieser einzelnen Aspekte eines Gebäudes wird zum „Agenten“ mit Vorlieben und Abneigungen > siehe Kaisersrot und Objekt Orientiertes Programmieren
| ||||
This website has been archived and is no longer maintained.